Understanding the Neural Tangent Kernel
A flurry of recent papers in theoretical deep learning tackles the common theme of analyzing neural networks in the infinite-width limit. At first, this limit may seem impractical and even pointless to study. However, it turns out that neural networks in this regime simplify to linear models with a kernel called the neural tangent kernel. Gradient descent is therefore very simple to study. While this may seem promising at first, empirical results show that neural networks in this regime perform worse than practical over-parameterized networks. Nevertheless, this still provides theoretical insight into some aspects of neural network training, so it is worth studying.
Additionally, this kernel regime can occur under a more general criterion which depends on the scale of the model, and does not require infinite width per se. In this post, I’ll present a simple and intuitive introduction to this theory that leads to a proof of convergence of gradient descent to 0 training loss. I’ll make use of a simple 1-d example which lends itself to neat visualizations to help make the ideas easier to understand.
Setup
Let’s start with an extremely simple example, and generalize our understanding once we get comfortable with this toy example. Let’s work with a 1-D input and 1-D output network. A simple 2-hidden layer relu network with width $m$ will do the trick for now.
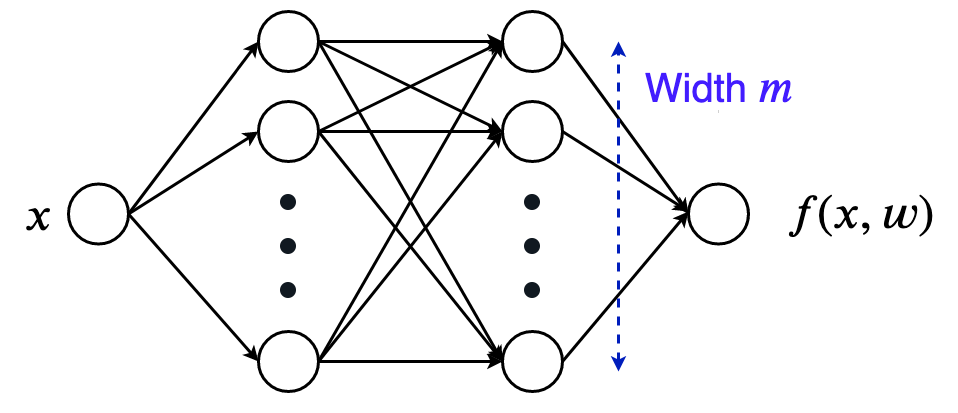
We can nicely plot how the network function looks for a bunch of random initializations:
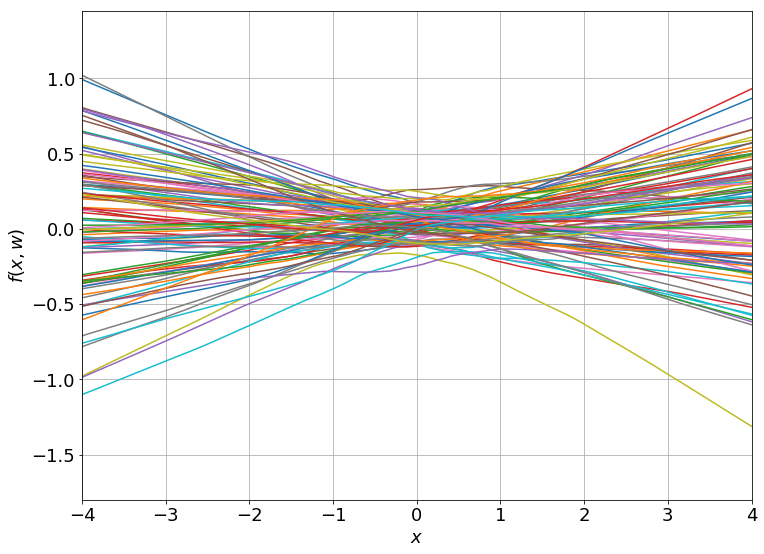
It turns out that these functions are equivalent to samples drawn from a Gaussian process as you take the hidden layer width to infinity, but that is a whole other can of worms best left for another post.
Let’s bring in some notation:
- Call the neural network function $f(x, \boldsymbol w)$ where $x$ is the input and $\boldsymbol w$ is the combined vector of weights (say of size $p$).
- In this 1-D example, our dataset will just be points $(x,y)$. Let’s say we have $N$ of them, so our dataset is: $\{ \bar x_i, \bar y_i \}_{i=1}^{N}$.
For learning the network, we’ll take a simple approach again: just perform full-batch gradient descent on the least squares loss. Now, you might be familiar with writing this loss as:
\[L(\boldsymbol w) = \frac{1}{N} \sum_{i=1}^{N} \frac{1}{2}(f(\bar x_i, \boldsymbol w) - \bar y_i)^2\]But we can simplify this using some vector notation.
- First, stack all the output dataset values $\bar y_i$ into a single vector of size $N$, and call it $\boldsymbol{\bar y}$.
- Similarly, stack all the model outputs for each input, $f(\bar x_i, \boldsymbol w)$ into a single prediction vector $\boldsymbol y(\boldsymbol w) \in \mathbb{R}^{N}$. We basically have $\boldsymbol y(\boldsymbol w)_i = f(\bar x_i, \boldsymbol w)$. This is similar in flavor to looking at the neural network function $f(\cdot, \boldsymbol w)$ as a single vector belonging to a function space.
- So, our loss simplifies to this:
Now, we won’t be changing the dataset size $N$ anywhere, and it’s an unnecessary constant in the loss expression. So, we can just drop it without affecting any of the further results, while making the algebra look less cluttered (we’ll keep the half because it will make the derivatives nicer).
\[L(\boldsymbol w) = \frac{1}{2} \Vert \boldsymbol y(\boldsymbol w) - \boldsymbol{\bar y} \Vert^2_2\]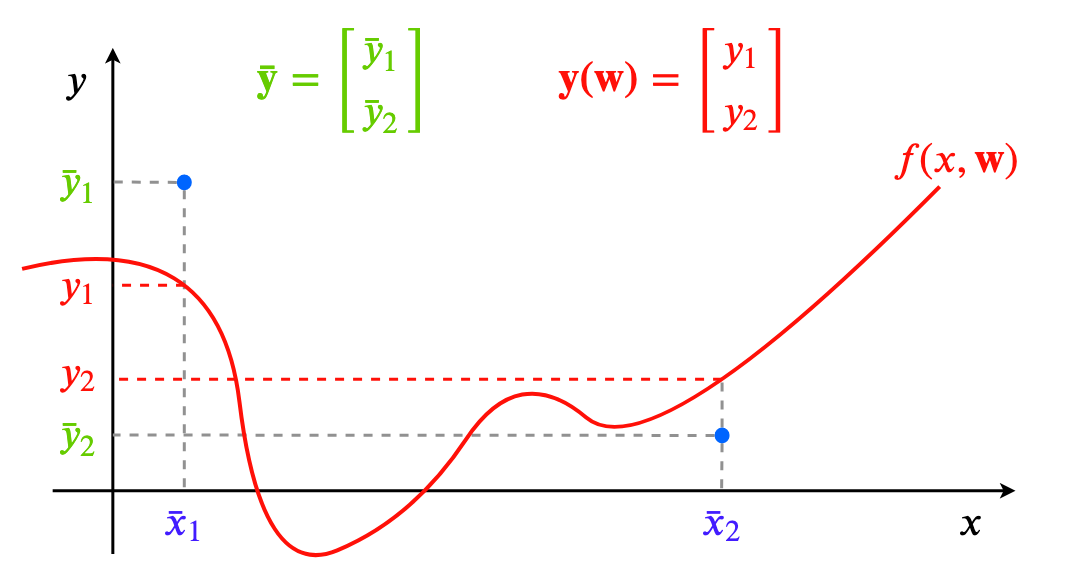
Training the network is now just minimizing this loss using gradient descent.
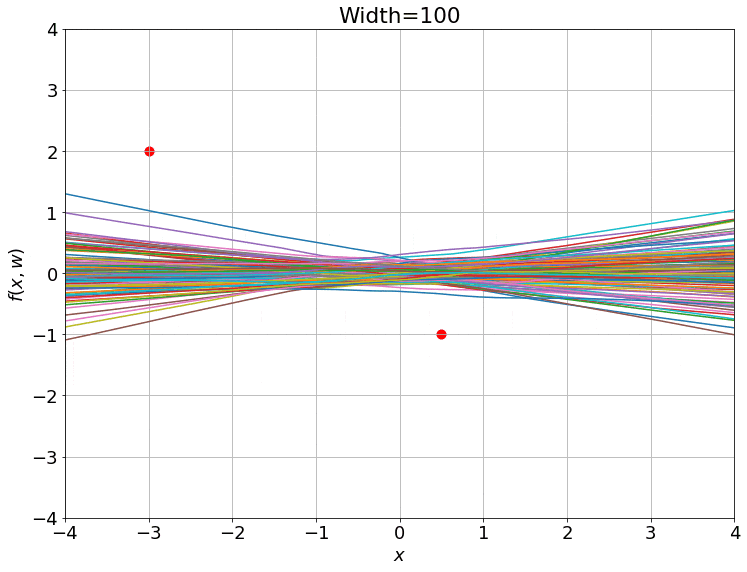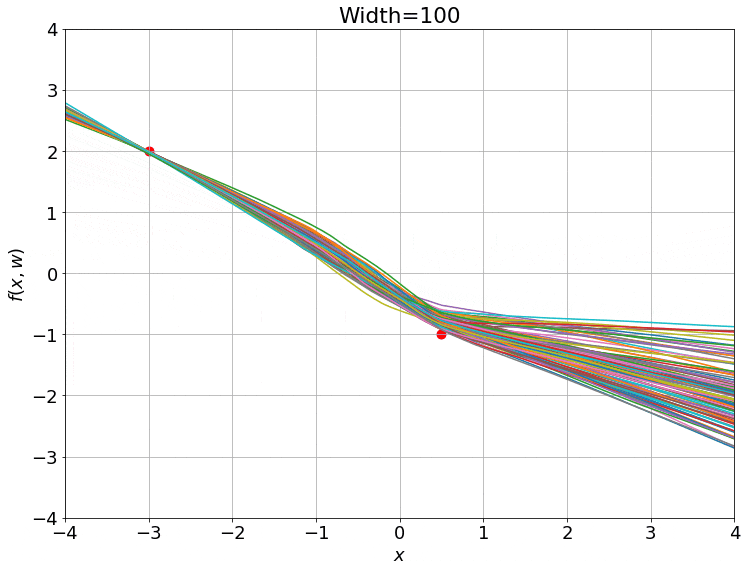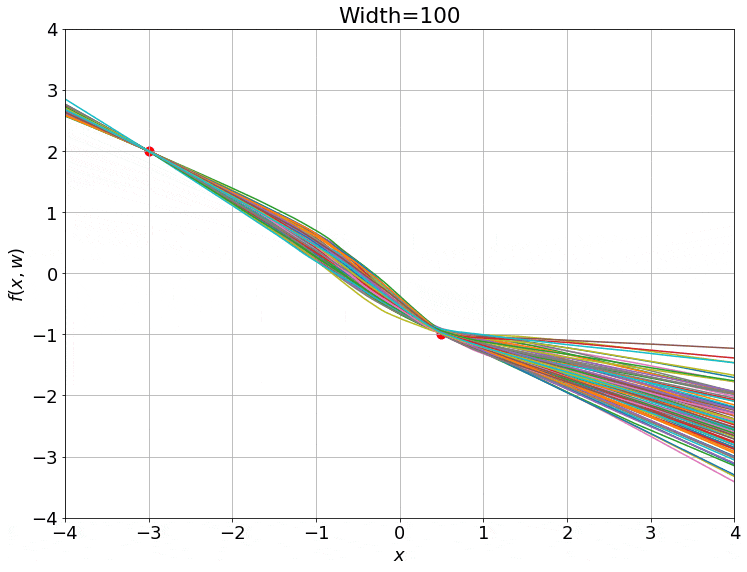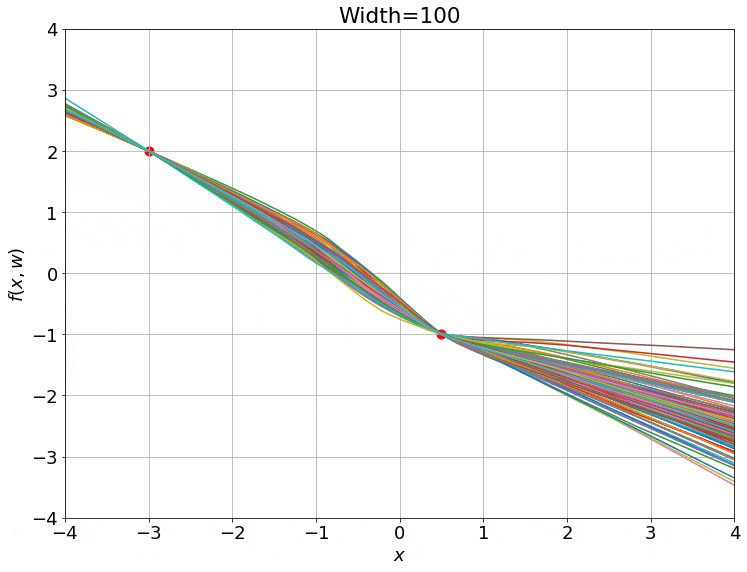
If we make a gif of the weights between the two hidden layers (an $m \times m$ matrix) as the training progresses, we observe something very intriguing:
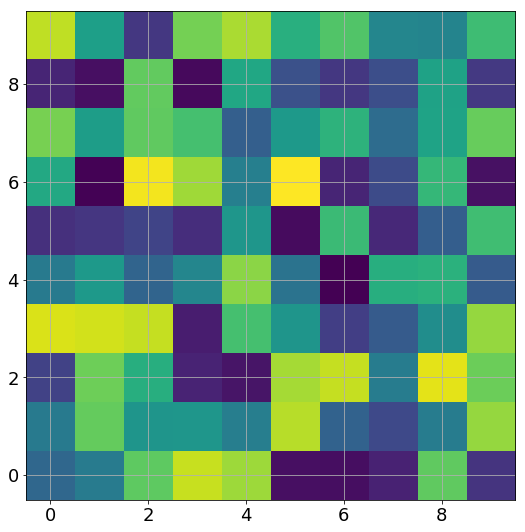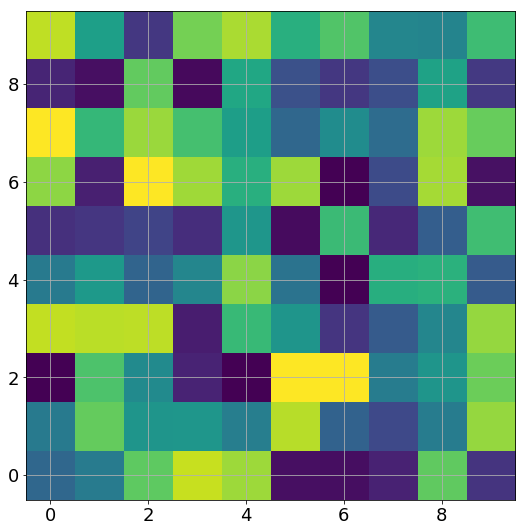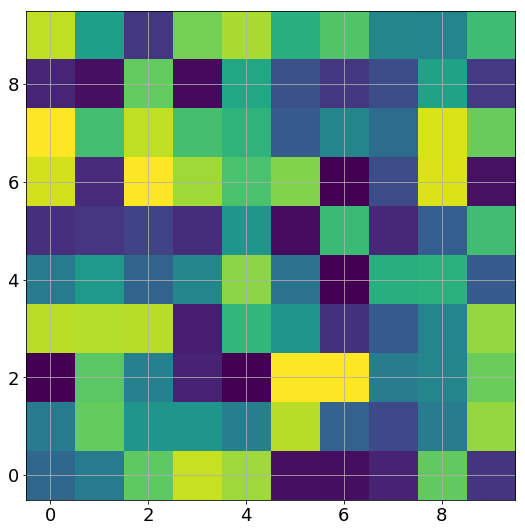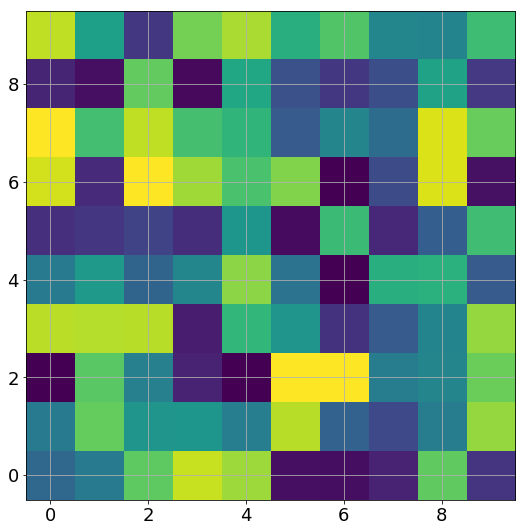
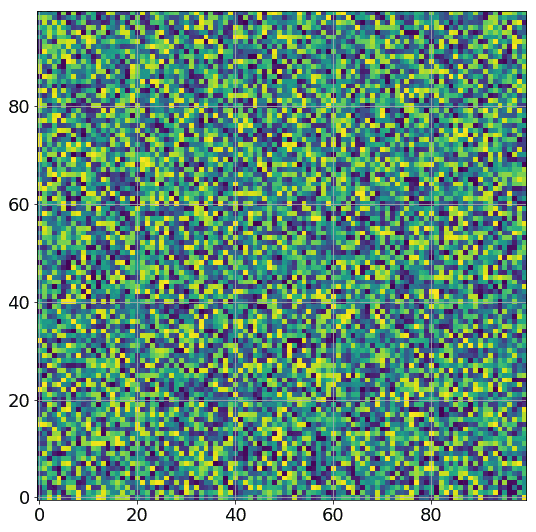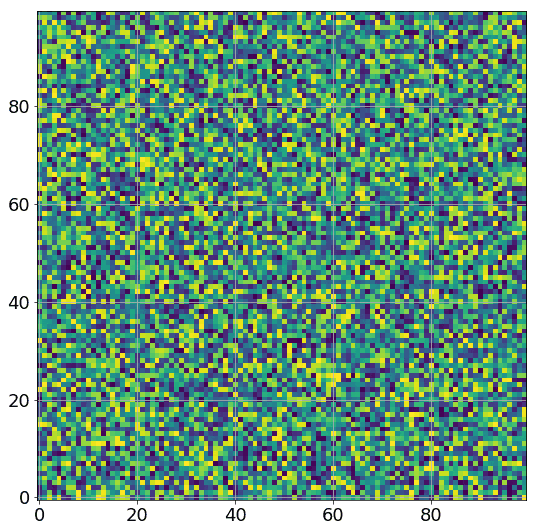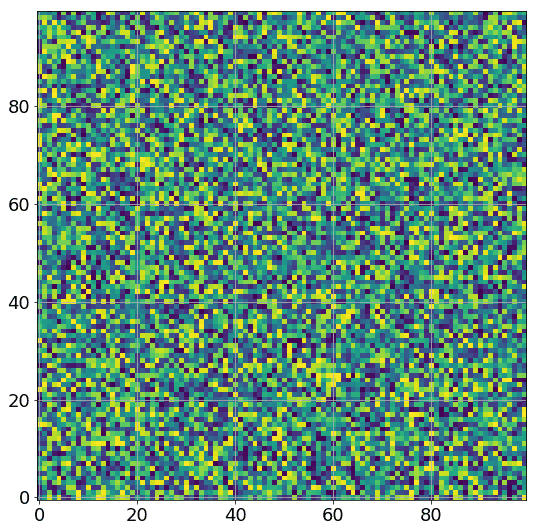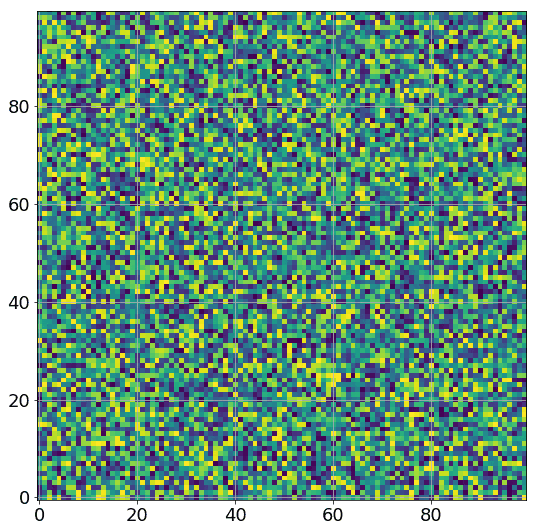
Yes, these are actually animated gifs, but the weights don’t even budge for larger widths! It seems that these models are quite lazy! We can see this quantitatively, by looking at the relative change in the norm of the weight vector from initialization:
\[\frac{\Vert \boldsymbol w(n) - \boldsymbol w_0 \Vert_2}{\Vert \boldsymbol w_0 \Vert_2}\]If the weights double, this relative change will be $2$ irrespective of the size of the hidden layers. Now if we plot this for the nets we trained above:
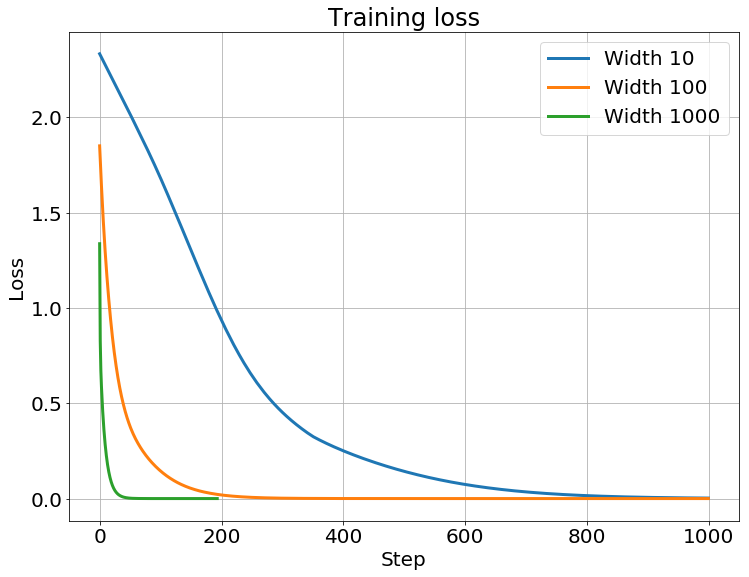
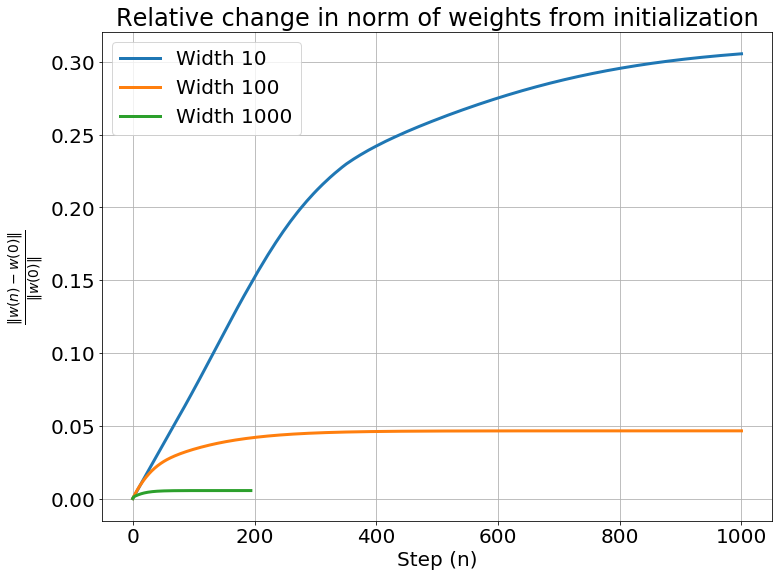
The weights don’t change much at all for larger hidden widths. Well, what’s a good thing to do if some variable doesn’t change much? Hint: Calc 101
Just Taylor Expand
That’s right, we can just Taylor expand the network function with respect to the weights around its initialization.
\[f(x, {\color{red}\boldsymbol w}) \approx f(x, \boldsymbol{w_0}) + \nabla_{\boldsymbol w}f(x, \boldsymbol{w_0})^T ({\color{red} \boldsymbol w} - \boldsymbol{w_0})\]We’ve turned the crazy non-linear network function into a simple linear function of the weights. Using our more concise vector notation for the model outputs on a specific dataset we can rewrite as:
\[\boldsymbol y({\color{red}\boldsymbol w}) \approx y(\boldsymbol{w_0}) + \nabla_{\boldsymbol w} \boldsymbol y(\boldsymbol{w_0})^T({\color{red}\boldsymbol w} - \boldsymbol{w_0})\]With matrix sizes made explicit:
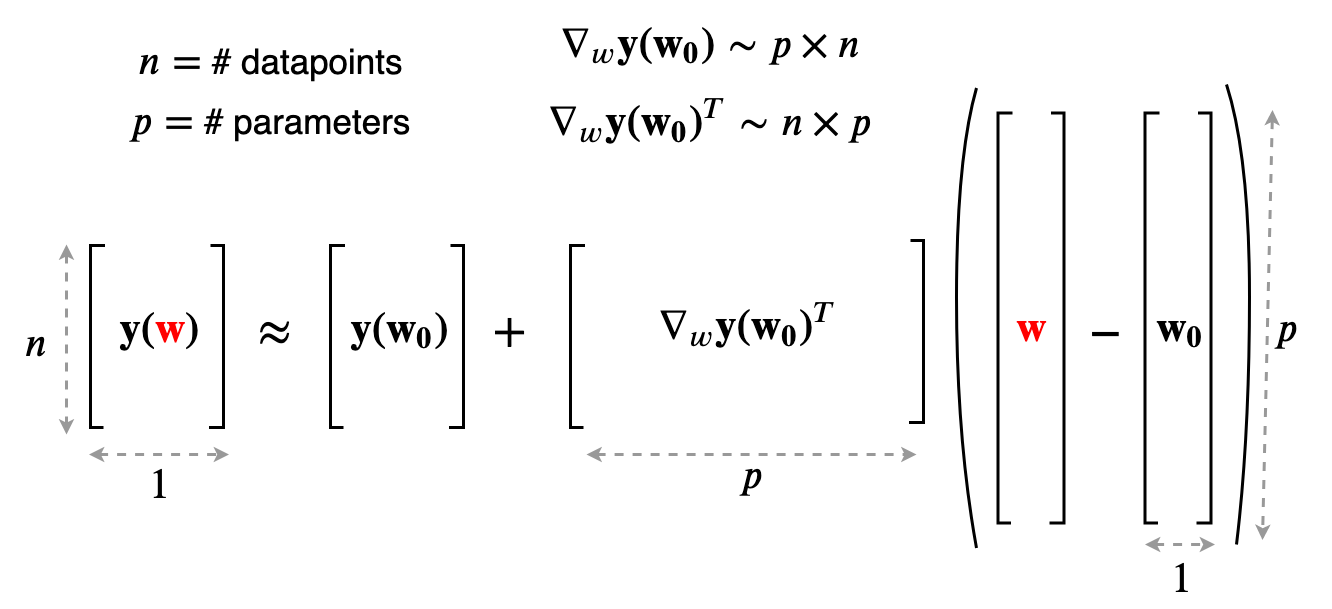
A lot of the things here like the initial output $y(\boldsymbol{w_0})$ and the model Jacobian $\nabla_{\boldsymbol w} \boldsymbol y(\boldsymbol{w_0})$ are just constants. Focus on the dependence on ${\color{red}\boldsymbol w}$ – the approximation is a linear model in the weights, so minimizing the least squares loss reduces to just doing linear regression! But, notice that the model function is still non-linear in the input, because finding the gradient of the model is definitely not a linear operation. In fact, this is just a linear model using a feature map $\boldsymbol \phi(x)$ which is the gradient vector at initialization:
\[\boldsymbol \phi({\color{blue}x}) = \nabla_{\boldsymbol w} f({\color{blue}x}, \boldsymbol{w_0})\]This feature map naturally induces a kernel on the input, which is called the neural tangent kernel. We’ll dive into the details of this kernel later when we look at gradient flows, but first, let’s try to theoretically justify this linear approximation.
When is the Approximation Accurate?
The linearized model is great for analysis, only if it’s actually an accurate approximation of the non-linear model. Let’s try to derive a quantitative criterion for when this approximation works well. This is adapted from Chizat and Bach’s paper on Lazy Training in Differentiable Programming (the lazy regime is just another name for when this linear approximation holds). You might need to brace yourself, because the derivation I’m presenting is intuitive and involves a bit of handwaving mixed with a salad of matrix and operator norms.
Firstly, we only care about the model being linear as we optimize it using gradient descent:
\[\boldsymbol w_1 = \boldsymbol w_0 - \eta \nabla_{\boldsymbol w} L(\boldsymbol w_0)\]With a small enough learning rate $\eta$, we know that the loss always decreases as we run gradient descent. So, the model outputs $\boldsymbol y(\boldsymbol{w_n})$ always get closer to the true labels $\boldsymbol{\bar y}$. Using this, we can bound the net change as follows:
\[\text{net change in }\boldsymbol y (\boldsymbol w) \lesssim \Vert \boldsymbol y(\boldsymbol{w_0}) - \boldsymbol{\bar y} \Vert\]Now we can quantify the “distance” we move in parameter space with a first order approximation,
\[\text{distance } d \text{ moved in $w$ space} \approx \frac{\text{net change in }\boldsymbol y (\boldsymbol w)}{\text{rate of change of } \boldsymbol y \text{ w.r.t }\boldsymbol w} = \frac{\Vert \boldsymbol y(\boldsymbol{w_0}) - \boldsymbol{\bar y} \Vert}{\Vert \nabla_w \boldsymbol y(\boldsymbol{w_0})\Vert}\]The norm of the Jacobian $\Vert \nabla_w \boldsymbol y(\boldsymbol{w_0})\Vert$ is an operator norm. If you aren’t familiar with operator norms, you can just think of it as a measure of the maximum stretching that a matrix can perform on a vector (or even simpler, just think of it as a measure of the ‘magnitude’ of the matrix).
To get the change in the Jacobian, we can use this distance $d$ along with the Hessian $\nabla_w^2 \boldsymbol y (\boldsymbol{w_0})$ of the model outputs with respect to the weights. This Hessian is a rank-3 tensor (still a linear operator) in our case, and you can think of it as stacking the Hessian matrices for each output together to get a 3-d Hessian “cuboid”. Again, think of its norm as just some measure of the magnitude of the Hessian, or the rate of change of the Jacobian.
\[\text{change in model Jacobian} \approx \text{distance } d \times \text{rate of change of the Jacobian} = d \cdot \Vert \nabla_w^2 \boldsymbol y (\boldsymbol{w_0})\Vert\]What we really care about when we want the model to be linear is not just the change in its Jacobian, but the relative change. Specifically, we want this relative change to be as small as possible ($\ll 1$):
\[\text{relative change in model Jacobian} \approx \frac{d \cdot \text{rate of change of Jacobian}}{\text{norm of Jacobian}} = \frac{d \cdot \Vert \nabla_w^2 \boldsymbol y (\boldsymbol{w_0})\Vert}{\Vert \nabla_w \boldsymbol y(\boldsymbol{w_0})\Vert} = {\color{blue} \Vert( \boldsymbol y (\boldsymbol w_0) - \boldsymbol{\bar y})\Vert \frac{\Vert \nabla_w^2 \boldsymbol {y(w_0)} \Vert}{\Vert \nabla_w \boldsymbol {y(w_0)} \Vert^2}}{\color{red} \ll 1}\]Let’s call the quantity in blue $\color{blue} \kappa(\boldsymbol{w_0})$. The condition $\color{blue} \kappa(\boldsymbol{w_0}) \color{red} \ll 1$ can be intuitively summarized as follows:
The amount of change in $\boldsymbol w$ required to produce a change of $\Vert( \boldsymbol y (\boldsymbol w_0) - \boldsymbol{\bar y})\Vert$ in $\boldsymbol y$ causes a negligible change in the Jacobian $\nabla_w \boldsymbol {y(w)}$.
This means that the model is very close to its linear approximation.
We now need to understand how $\color{blue} \kappa(\boldsymbol{w_0})$ changes with the hidden width $m$ of our neural network. It turns out that $\color{blue} \kappa \to 0$ as the width $m \to \infty$. We need to be a bit careful here, because $\kappa(\boldsymbol{w_0})$ is a random variable as the initialization $\boldsymbol{w_0}$ is itself random. What I mean when I say $\kappa \to 0$ is that its expectation goes to 0. This only holds if the weights are properly initialized. Specifically, they need to be independent zero-mean Gaussian random variables with a variance that goes inversely with the size of the input layer. (This is called LeCun initialization, more on this in the next section). This result explains why the weights changed less while training for larger width neural networks.
Understanding why this result is true for the general case is quite complicated, so I’ll present a derivation for the simpler case of only one hidden layer.
An intuitive explanation for why this happens is as follows: a large width means that there are a lot more neurons affecting the output. A small change in all of these neuron weights can result in a very large change in the output, so the neurons need to move very little to fit the data. If the weights move less, the linear approximation is more accurate. As the width increases, this amount of neuron budging decreases, so the model gets closer to its linear approximation. If you are happy with just believing this intuition, you can skip the proof and go to the next section.
One Hidden Layer Network proof (click to expand)
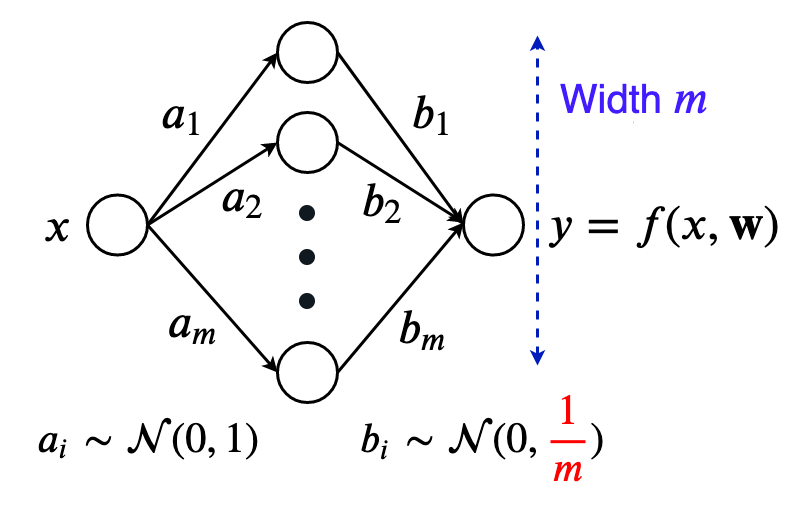
Let's look at a one hidden layer neural network, again with 1-d inputs and outputs, and no biases to make our life simpler. The network function is simply: $$f(x, \boldsymbol w) = \sum_{i=1}^m b_i \sigma (a_i x)$$ Where,- $\sigma$ is a smooth twice-differentiable activation function. (Note: ReLU is not twice differentiable, but we can approximate it with a smooth version and everything more or less works out).
- The layer weights $a_i$ and $b_i$ are stacked into a parameter vector $w \in \mathbb{R}^{2m}$.
- $a_i \sim \mathcal{N}(0, 1)$
- $b_i \sim \mathcal{N}(0, {\color{red}\frac{1}{m}})$ (adding $m$ of these gives unit variance)
To analyze the width asymptotics of $\color{blue} \kappa(\boldsymbol{w_0})$, we need to find the model Jacobian and Hessians, which are a matrix and a rank-3 tensor in general. Sticking with the theme of simplifying, we will restrict our analysis to a dataset of just one point $(x, \bar y)$, so that the Jacobian becomes a simple gradient vector and the Hessian becomes a matrix. Our output therefore is just a scalar: $y(\boldsymbol{w_0}) = f(x, \boldsymbol{w_0})$.
Okay, now that we have all the simplifications settled, let's deal with $\color{blue} \kappa(\boldsymbol{w_0})$ piece by piece. Remember that we're only interested in the asymptotics of $\color{blue} \kappa(\boldsymbol{w_0})$ as the width $m \to \infty$.
First off, because of our specific initialization, the model output stays more or less constant with width, so $\Vert y(\boldsymbol {w_0}) - \bar y \Vert\sim \mathcal{O}(1)$ (interpret the big-O notation as the expected asymptotic behavior when width $m \to \infty$). This means that we can just ignore this term, and we're left with the following ratio: $$\kappa(w_0) \sim \frac{\text{norm of Hessian}}{\text{(norm of gradient)}^2}$$Let's deal with the two terms one at a time.
Gradient
Finding the gradient is just a matter of applying the chain rule (which is essentially back-propping by hand for two layers). The output is: $$y = \sum_{i=1}^m b_i \sigma (a_i x)$$ I've dropped $\boldsymbol{w_0}$ because all the derivatives will be evaluated at the initialization, so it's just unnecessary clutter.We can write down the gradients for the two layers:
$$\frac{\partial y}{\partial a_i} = {\color{red}b_i} \cdot \sigma'(a_i x) x \text{ and }\frac{\partial y}{\partial b_i} = \sigma(a_i x)$$ Where $\sigma'$ is the derivative of the activation. The gradient norm is: $$\Vert \nabla y \Vert = \sqrt{\left( \frac{\partial y}{\partial a_1} \right)^2 + \dots + \left( \frac{\partial y}{\partial a_m} \right)^2 + \left( \frac{\partial y}{\partial b_1} \right)^2 + \dots + \left( \frac{\partial y}{\partial b_m} \right)^2}$$ Notice that:- $x$ is just a constant that we can assume is bounded.
- $\sigma(a_i x)$ and $\sigma'(a_i x)$ are random variables with constant variances as the width increases. (We need $\sigma$ to be Lipschitz for this.)
- Only the variance of $\color{red} b_i$ varies with width. Specifically, it goes as $\mathcal{O}(\frac{1}{m})$ because of LeCun initialization.
- $m$ variables with mean $\mathcal{O}(\frac{1}{m})$ (the $\big( \frac{\partial y}{\partial a_i}\big)^2$). These go to 0 as $m \to \infty$, so we can just ignore them.
- Another $m$ variables with mean $\mathcal{O}(1)$ (the $\big( \frac{\partial y}{\partial b_i}\big)^2$).
Recall that big-$\Omega$ is the same as big-O, but an asymptotic lower bound instead of an upper bound. We need a lower bound for the gradient norm because it is in the denominator of the expression for $\kappa$ (which we are trying to upper bound).
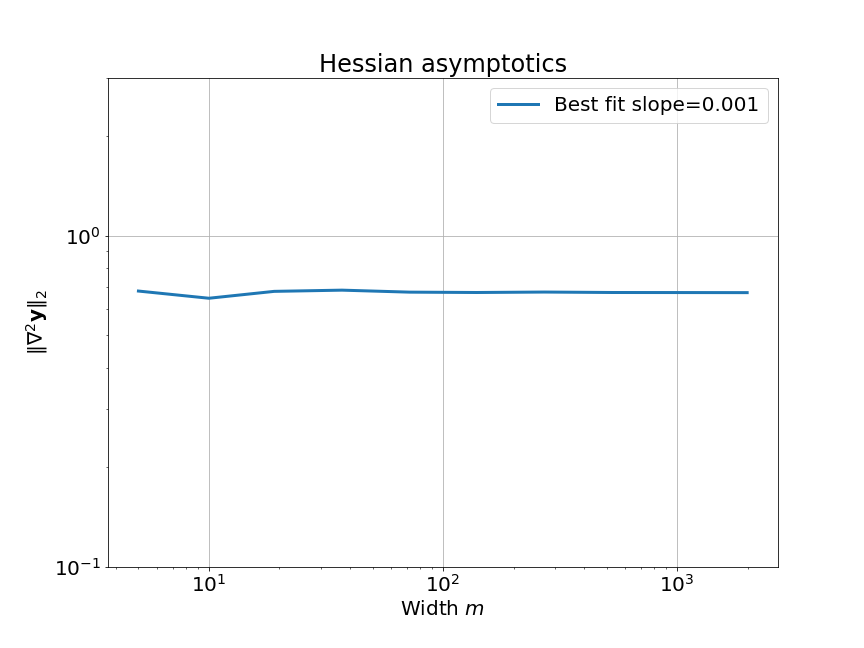
We can empirically verify this asymptotic behavior pretty easily: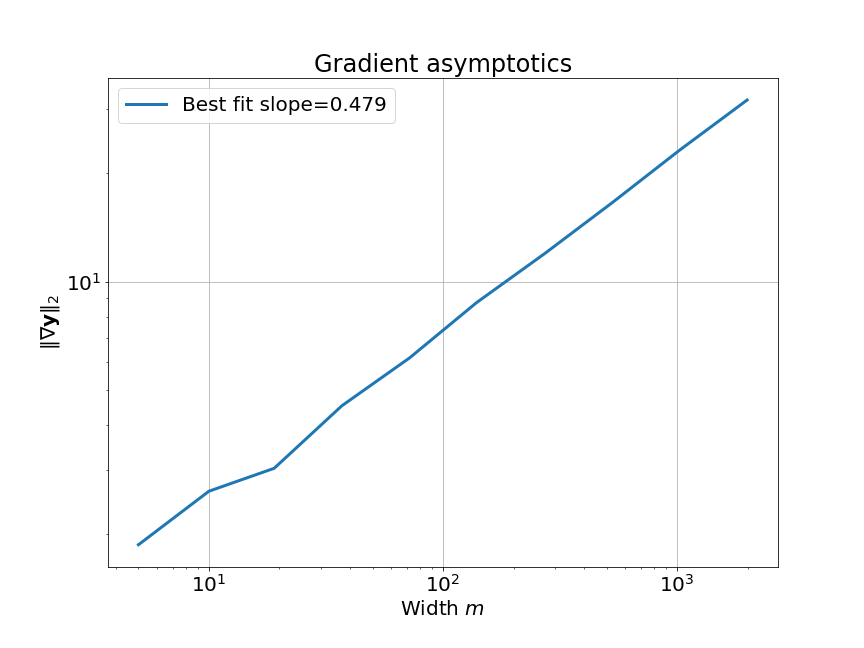
Hessian
We're almost there, just another derivative. This might seem a bit daunting at first, but it will simply involve a bit more differentiation. First off, the gradient vector has two blocks ($\boldsymbol a$ and $\boldsymbol b$ are the weight vectors for the first and second layers): $$\nabla y = \begin{bmatrix}\frac{\partial y}{\partial \boldsymbol a} \\ \frac{\partial y}{\partial \boldsymbol b} \end{bmatrix}$$ Therefore, the Hessian will have this structure: $$\nabla^2 y = \begin{bmatrix} \frac{\partial^2 y}{\partial \boldsymbol a^2} & \frac{\partial^2 y}{\partial \boldsymbol b \partial \boldsymbol a} \\ \frac{\partial^2 y}{\partial \boldsymbol a \partial \boldsymbol b} & \frac{\partial^2 y}{\partial \boldsymbol b^2} \end{bmatrix}$$ Let's find these blocks one by one. Recall the gradients: $$\frac{\partial y}{\partial a_i} = {\color{red}b_i} \cdot \sigma'(a_i x) x \text{ and }\frac{\partial y}{\partial b_i} = \sigma(a_i x)$$ First, the blocks on the diagonal: $$ \begin{align*} \frac{\partial}{\partial a_j} \left( \frac{\partial y}{\partial a_i} \right) &= \frac{\partial}{\partial a_j} ({\color{red}b_i} \cdot \sigma'(a_i x) x) \\ &= {\color{red}b_i} \cdot \sigma''(a_i x) x^2 \text{ if } i=j \text{ and 0 otherwise} \end{align*} $$ Where $\sigma''$ is the second derivative of the activation. Now, the next block on the diagonal is: $$\frac{\partial}{\partial b_j} \left( \frac{\partial y}{\partial b_i} \right) = \frac{\partial}{\partial b_j} (\sigma(a_i x)) = 0$$ So the first block on the diagonal is a nice diagonal matrix and the second block is completely 0. The two off-diagonal blocks must be equal because the Hessian is symmetric, so we only need to find one of them. $$ \begin{align*} \frac{\partial}{\partial a_j} \left( \frac{\partial y}{\partial b_i} \right) &= \frac{\partial}{\partial a_j} (\sigma(a_i x)) \\ &= \sigma'(a_i x) x \text{ if } i=j \text{ and 0 otherwise} \end{align*} $$Again, these blocks are also nice diagonal matrices. Now, the only term with $\color{red} b_i$ is the first diagonal block. Only these entries have a variance that goes as $\mathcal{O}(\frac{1}{m})$, while the two off-diagonal blocks have entries with constant variances. This picture should make it clear:
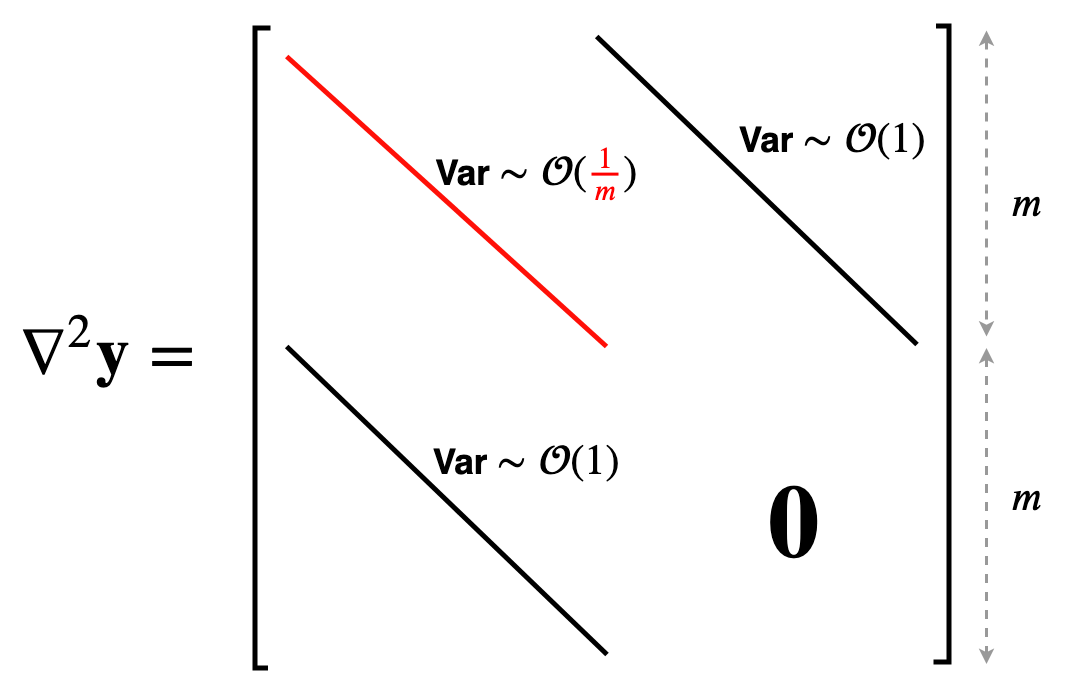
We need to find the operator norm of this matrix. The operator norm doesn't change if we swap around rows (because that is an orthogonal transformation), so we can instead find the norm of this nice lower triangular matrix:
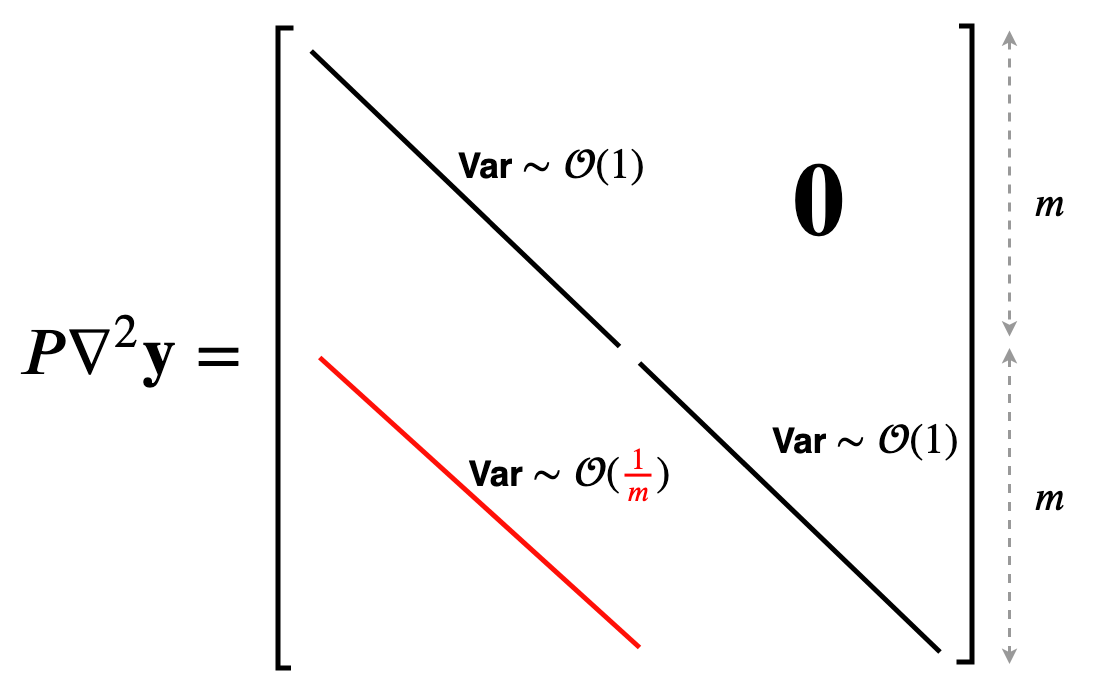
Putting it Together
Now it is just a matter of substituting in the expression for $\kappa$: $$\kappa(w_0) \sim \frac{\text{norm of Hessian}}{\text{(norm of gradient)}^2} \sim \frac{\color{purple}\mathcal{O}(1)}{\color{green}\Omega(\sqrt{m})^2} \sim \color{red}\mathcal{O}\left(\frac{1}{m}\right)$$ Clearly, this means that $\kappa \to 0$ as $m \to \infty$. In other words, the linear approximation is better for larger widths! We can confirm this for a tanh network: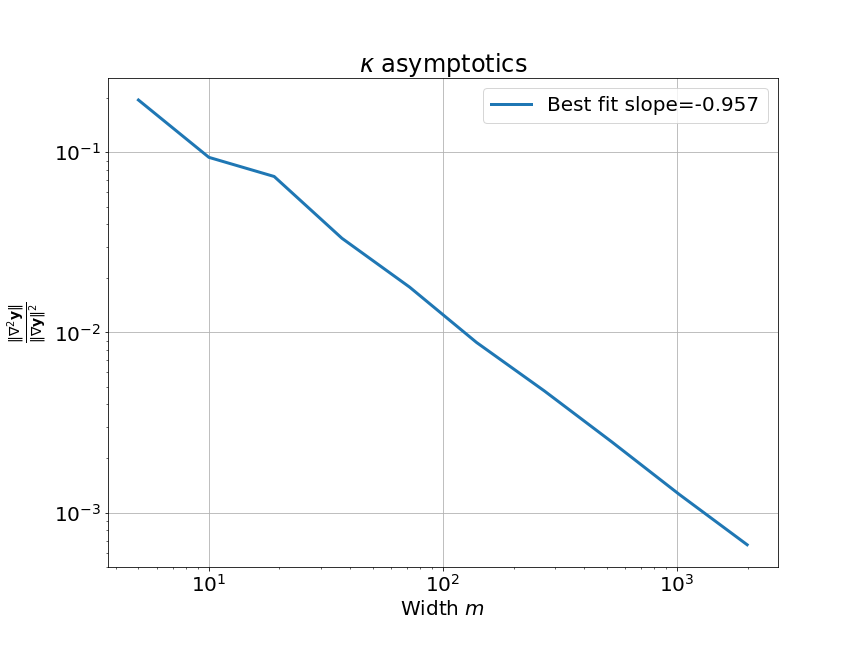
I didn't want to present all the details of this proof and wanted to focus on the intuitive arguments, so I hope you won't send your mathematical lawyers to sue me.
Some comments:- LeCun initialization is crucial for this condition to hold. If we choose a smaller initialization variance, the network will not approach the linear regime with infinite width.
- This derivation was for just one value of input $x$, but you can easily extend it to larger dataset sizes using some simple results on the norms of block matrices.
- I ignored biases, but they won't affect the final result and are fairly easy to take into account as well.
- Dealing with higher dimensional inputs and outputs is also doable in the same vein, but the algebra gets quite hairy.
- Extending to multiple layers is not trivial, but the result still holds. It roughly involves inducting on the layers by sending their widths to infinity one by one, and keeping track of gradients using back-prop equations. If you're brave enough, you can dive into the proofs in the Neural Tangent Kernel paper, or perhaps the proof in the paper On Exact Computation in an Infinitely Wide Net might seem marginally more approachable.
While this is a nifty result for when a neural net behaves linearly in its parameters, it turns out that a much simpler and general condition is easy to derive.
Scaling the Output
Let’s stare at the expression for $\color{blue} \kappa(\boldsymbol{w_0})$ again:
\[\color{blue} \kappa(\boldsymbol{w_0}) = {\color{blue} \Vert( \boldsymbol y (\boldsymbol w_0) - \boldsymbol{\bar y})\Vert \frac{\Vert \nabla_w^2 \boldsymbol {y(w_0)} \Vert}{\Vert \nabla_w \boldsymbol {y(w_0)} \Vert^2}}\]I’m going to do a very simple thing, just multiply the output of our model by some factor $\alpha$.
\[\kappa_{\color{red}\alpha}(\boldsymbol{w_0}) = { \Vert( {\color{red}\alpha}\boldsymbol y (\boldsymbol {w_0}) - \boldsymbol{\bar y})\Vert \frac{\Vert \nabla_w^2 {\color{red}\alpha}\boldsymbol {y(w_0)} \Vert}{\Vert \nabla_w {\color{red}\alpha}\boldsymbol {y(w_0)} \Vert^2}}\]Yup, this is literally just rescaling the model. The $\Vert( \boldsymbol y (\boldsymbol {w_0}) - \boldsymbol{\bar y})\Vert$ term is annoying, and we can get rid of it by assuming that our model always outputs 0 at initialization, i.e. $\boldsymbol y (\boldsymbol {w_0}) = 0$. (We can make any model have this behavior by subtracting a copy of it at initialization.)
\[\implies \kappa_{\color{red}\alpha}(\boldsymbol{w_0}) \sim \frac{\Vert \nabla_w^2 {\color{red}\alpha} \boldsymbol {y(w_0)} \Vert}{\Vert \nabla_w {\color{red}\alpha} \boldsymbol {y(w_0)} \Vert^2} = \frac{ {\color{red}\alpha} \Vert \nabla_w^2 \boldsymbol {y(w_0)} \Vert}{ {\color{red}\alpha^2}\Vert \nabla_w \boldsymbol {y(w_0)} \Vert^2} = {\color{red}\frac{1}{\alpha}}{ \frac{\Vert \nabla_w^2 \boldsymbol {y(w_0)} \Vert}{\Vert \nabla_w \boldsymbol {y(w_0)} \Vert^2}}\]We can make the model linear (take $\color{blue}\kappa(\boldsymbol{w_0}) \to 0$) by simply jacking up $\color{red} \alpha \to \infty $! Following this, the authors of the paper on lazy training called this quantity $\kappa(w_0)$ the inverse relative scale of the model.
One important thing to notice is that this works for any non-linear model, and is not specific to neural networks (needs to be twice differentiable though). So, to visualize this, I cooked up a crazy 1-D example model. This model has one weight $w$ initialized to $w_0 = 0.4$.
\[f(x, w) = (wx + w^2 x + \sin(e^{0.1w}))(w - 0.4)\]It also satisfies our requirement that the output be 0 at initialization. To see the effect of $\color{red} \alpha$ on the linearity of the model, we can just look at the value of the function at one specific value of $x$, say $x = 1.5$. Varying $\color{red} \alpha$, we get:
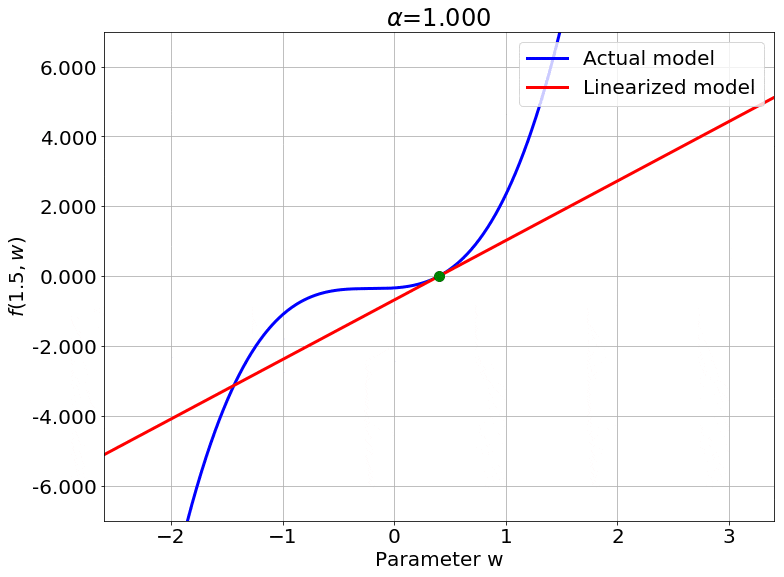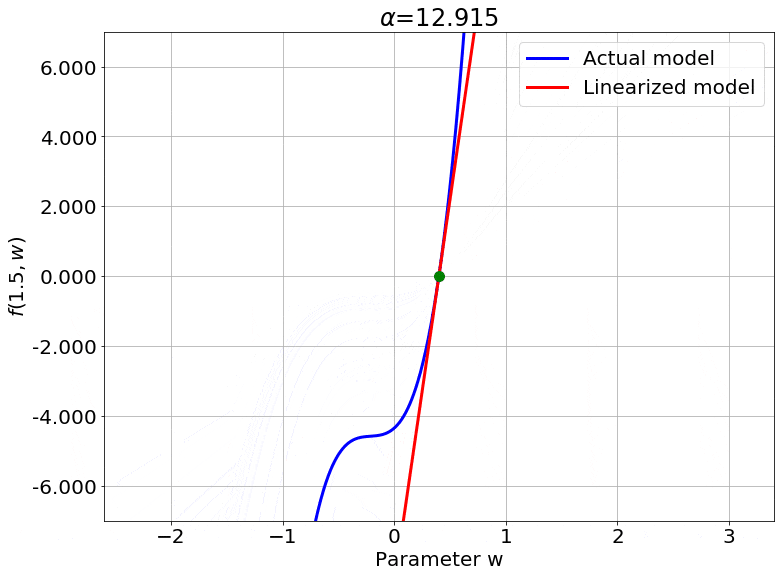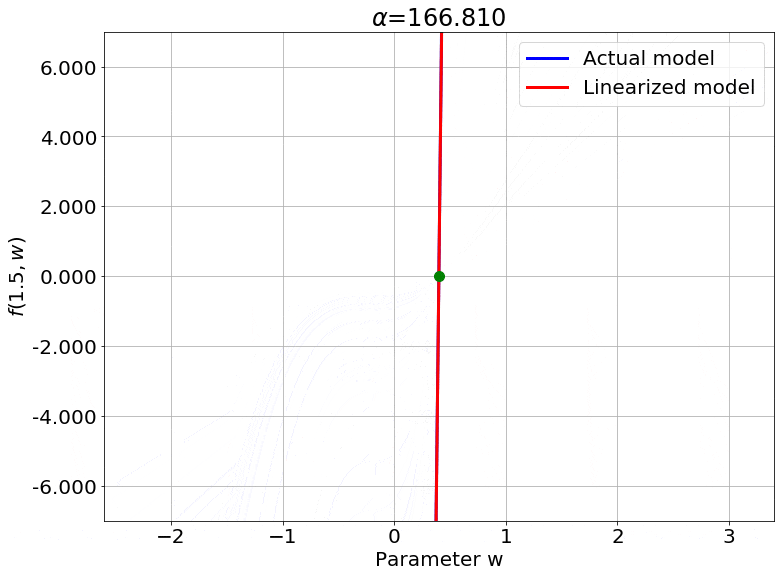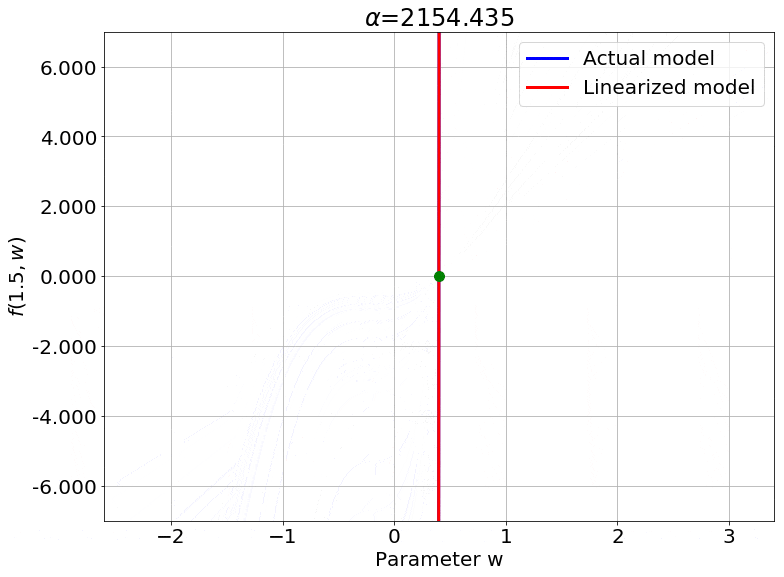
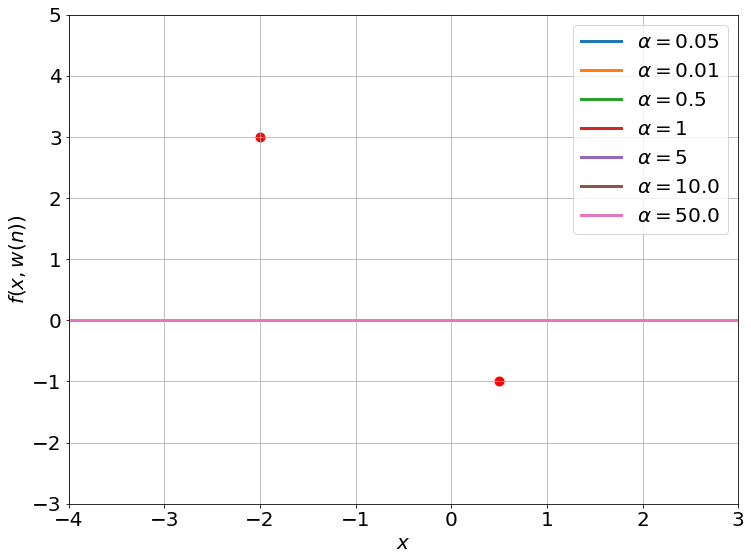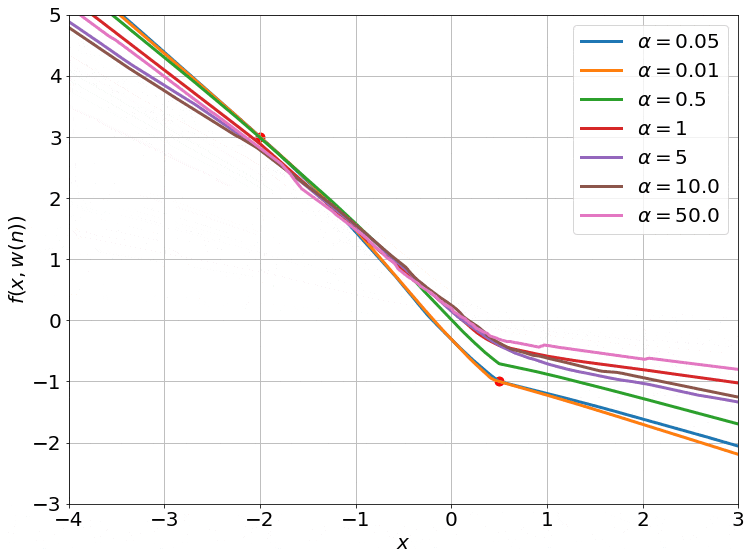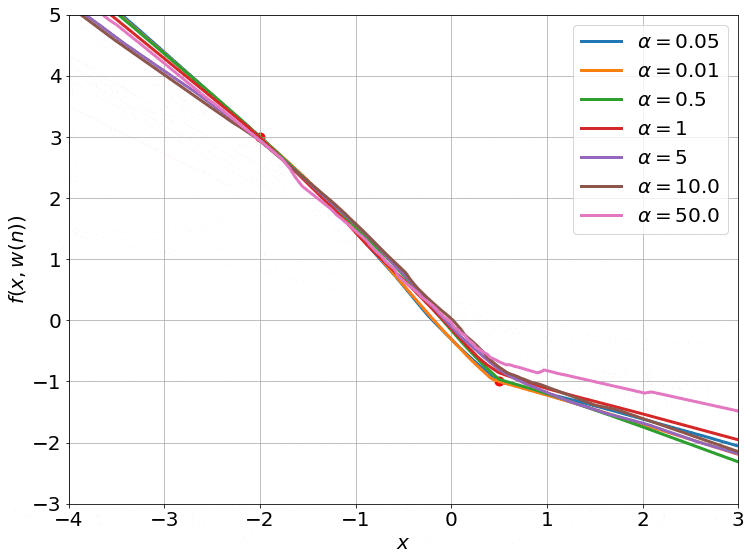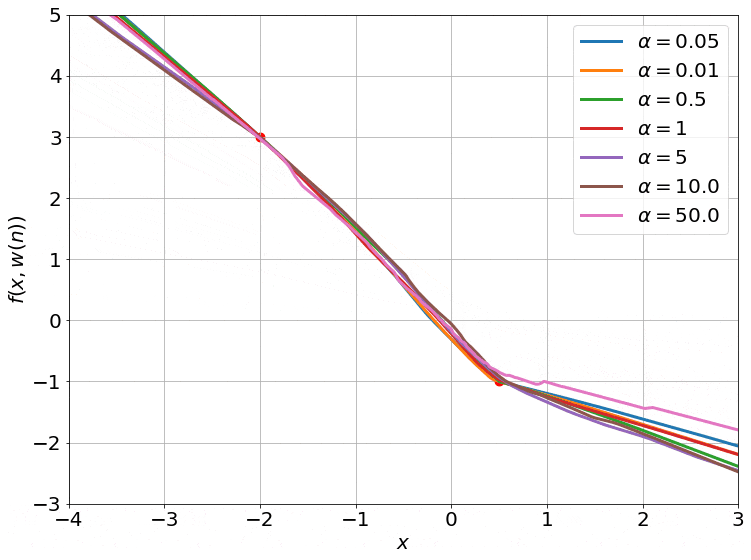
We can also look at the loss surface for a single data point for the two models. The linearized loss would be a nice parabola, and we would expect the actual loss to get closer to this parabola with increasing $\color{red} \alpha$:
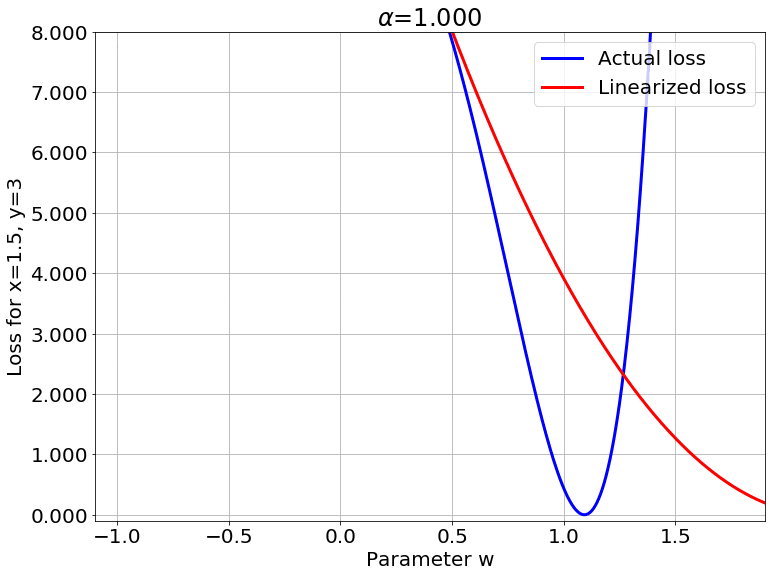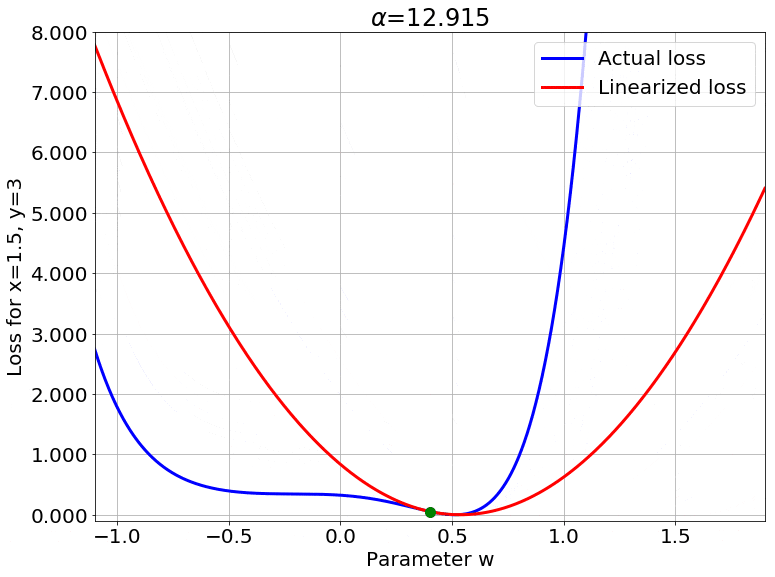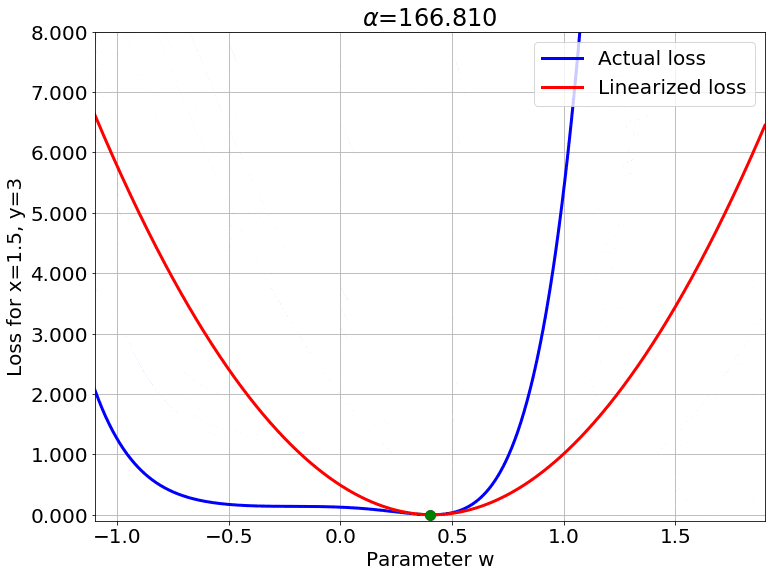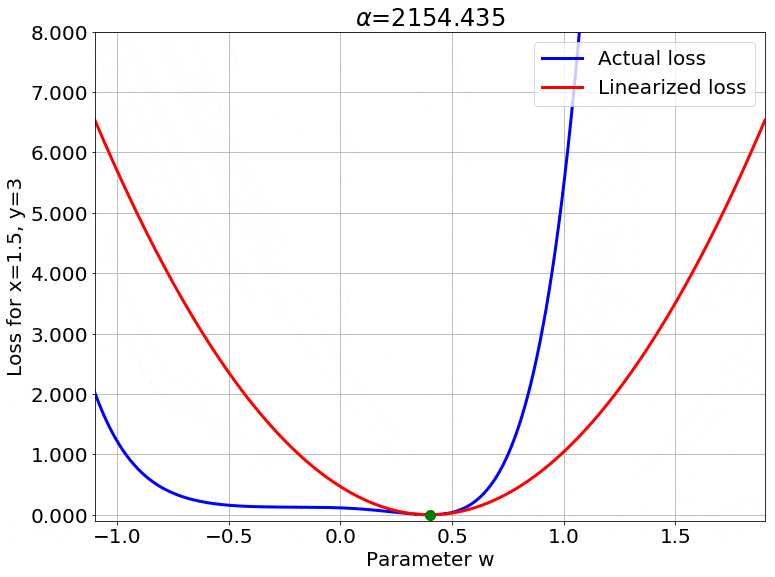
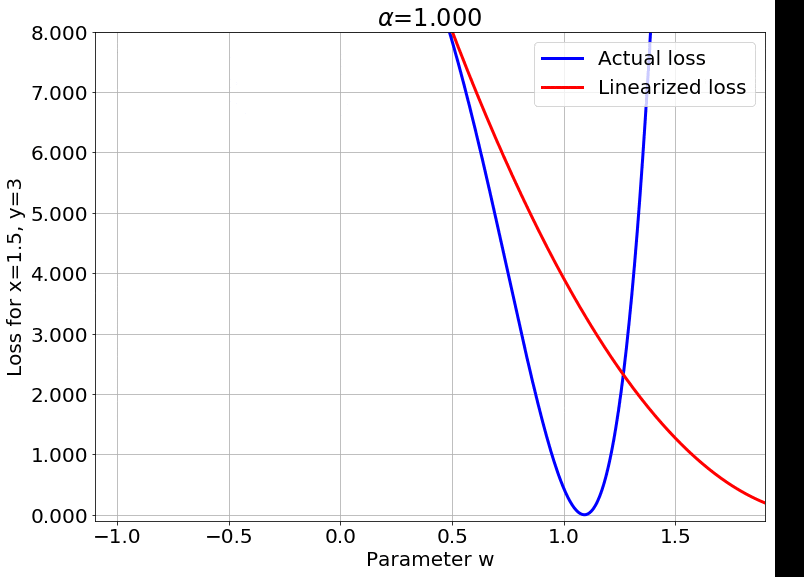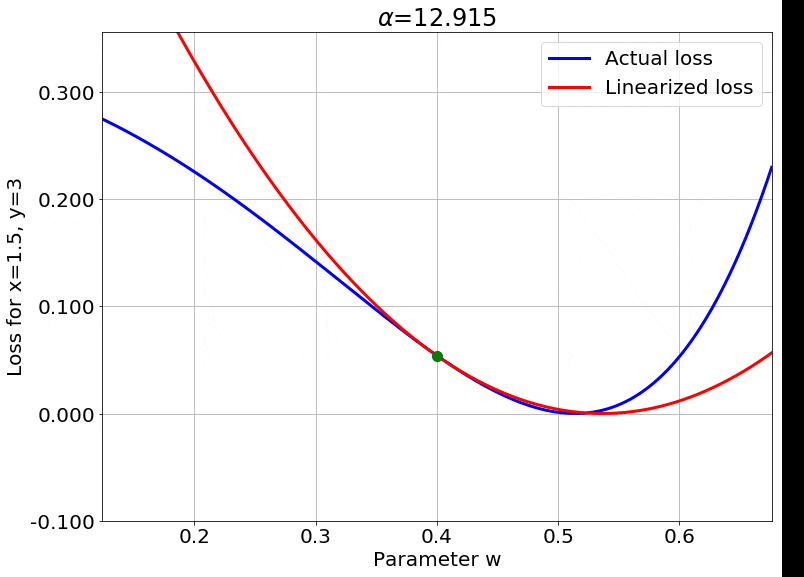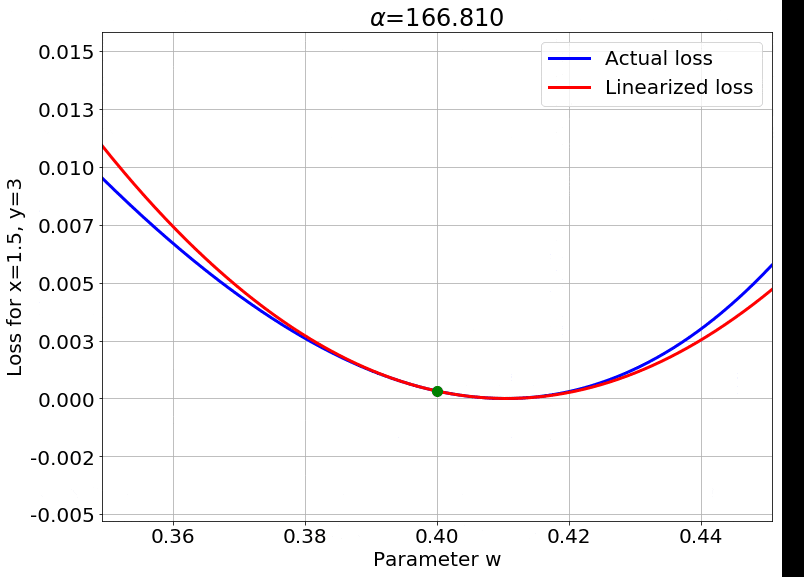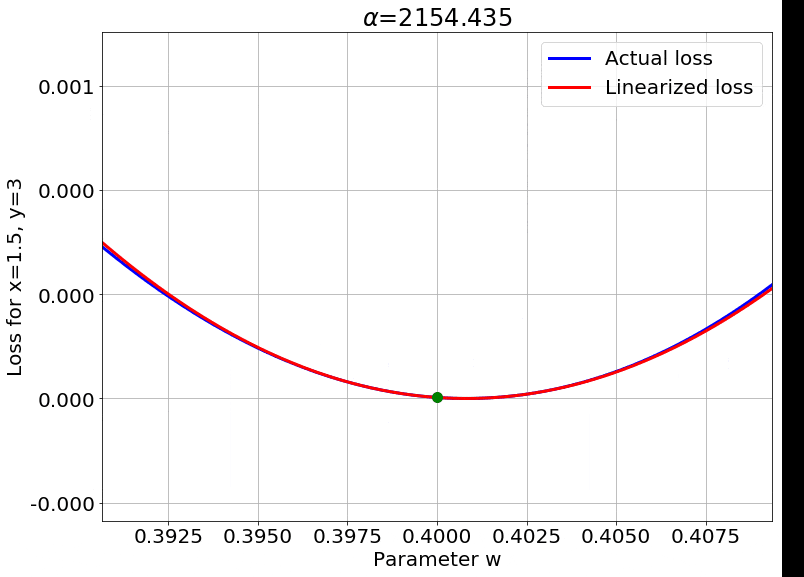
A couple of important observations:
- The linearized loss does get closer to the actual loss as we expected.
- The minima of the two loss surfaces also get closer, and more importantly, they get closer to the initialization as well. This perfectly agrees with our earlier observations that the weights barely budge as we train the model.
Gradient Flow
We’ve settled the question of when neural networks and more general non-linear models are accurately approximated by their linearizations. Let’s now get into their training dynamics under gradient descent.
\[\boldsymbol w_{k+1} = \boldsymbol w_k - \eta \nabla_{\boldsymbol w} L(\boldsymbol w_k)\]Rewriting this equation a bit, we get:
\[\frac{\boldsymbol w_{k+1} - \boldsymbol w_{k}}{\eta} = -\nabla_{\boldsymbol w} L(\boldsymbol w_k)\]The term on the left hand side looks like a finite-difference approximation to a derivative. And this equation is like a difference equation approximation to a differential equation. If we take the learning rate to be infinitesimally small, we can look at the evolution of the weight vectors over time, and write down this differential equation:
\[\frac{d \boldsymbol w(t)}{dt} = -\nabla_{\boldsymbol w} L(\boldsymbol w(t))\]This is called a gradient flow. In essence, it is a continuous time equivalent of standard gradient descent. The main point is that the trajectory of gradient descent in parameter space closely approximates the trajectory of the solution of this differential equation if the learning rate is small enough. To simplify notation, I will denote time derivatives with a dot: $\frac{d \boldsymbol w(t)}{dt} = \boldsymbol {\dot w}(t)$. The gradient flow is:
\[\boldsymbol{\dot w}(t) = - \nabla L(\boldsymbol{w}(t))\]Additionally, let’s drop the time variable as it can be inferred from context. Substituting for the loss and taking the gradient, we get:
\[\boldsymbol{\dot w} = - \nabla \boldsymbol{y}(\boldsymbol{w}) (\boldsymbol{y}(\boldsymbol{w}) - \boldsymbol{\bar y})\]We can now derive the dynamics of the model outputs $\boldsymbol{y}(\boldsymbol{w})$ (this is basically the dynamics in function space) induced by this gradient flow using the chain rule:
\[\dot{\boldsymbol{y}}(\boldsymbol{w}) = \nabla \boldsymbol{y}(\boldsymbol{w})^T \boldsymbol{\dot w} = - {\color{red}\nabla \boldsymbol{y}(\boldsymbol{w})^T \nabla \boldsymbol{y}(\boldsymbol{w})} (\boldsymbol{y}(\boldsymbol{w}) - \boldsymbol{\bar y})\]The quantity in red, $\color{red} \nabla \boldsymbol{y}(\boldsymbol{w})^T \nabla \boldsymbol{y}(\boldsymbol{w})$ is called the neural tangent kernel (NTK for short). Let’s give it a symbol $\color{red} \boldsymbol{H}(\boldsymbol{w})$.
If you go back to the part where we first Taylor expanded the network function, we saw that the linearized model has a feature map $\boldsymbol \phi({\color{blue}x}) = \nabla_{\boldsymbol w} f({\color{blue}x}, \boldsymbol{w_0})$. The kernel matrix corresponding to this feature map is obtained by taking pairwise inner products between the feature maps of all the data points. This is exactly $\boldsymbol{H}(\boldsymbol{w_0})$!
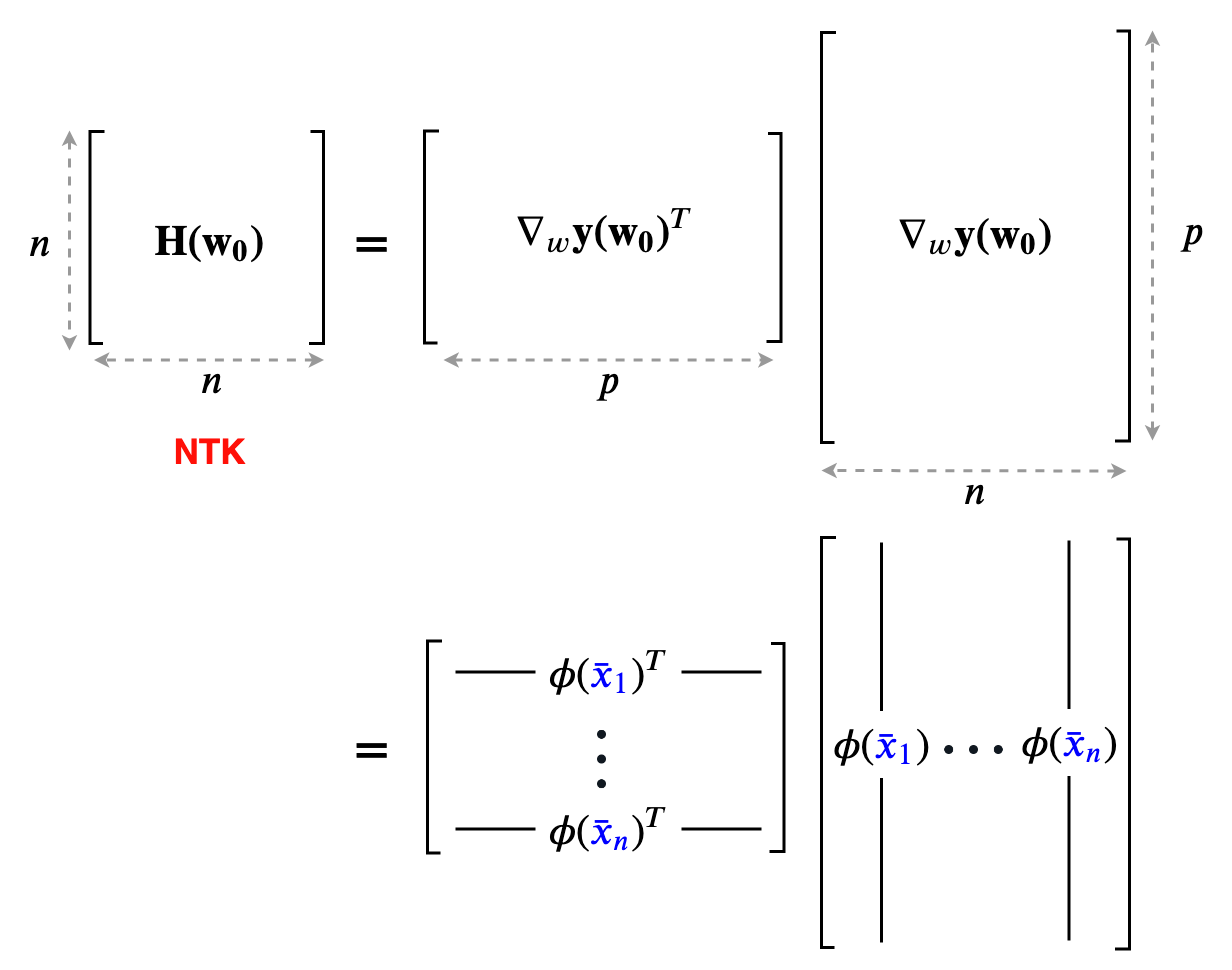
If the model is close to its linear approximation, ($\color{blue}\kappa(\boldsymbol{w_0}) \ll 1$), the Jacobian of the model outputs does not change as training progresses. In other words,
\[\nabla \boldsymbol{y}(\boldsymbol{w}(t)) \approx \nabla \boldsymbol{y}(\boldsymbol{w}_0) \implies \boldsymbol{H}(\boldsymbol{w}(t)) \approx \boldsymbol{H}(\boldsymbol{w}_0)\]This is referred to as the kernel regime, because the tangent kernel stays constant during training. The training dynamics now reduces to a very simple linear ordinary differential equation:
\[\dot{\boldsymbol{y}}(\boldsymbol{w}) = - \boldsymbol{H}(\boldsymbol{w_0}) (\boldsymbol{y}(\boldsymbol{w}) - \boldsymbol{\bar y})\]Clearly, $\boldsymbol{y}(\boldsymbol{w}) = \boldsymbol{\bar y}$ is an equilibrium of this ODE, and it corresponds to a train loss of 0 – exactly what we want. We can change state variables to get rid of $\boldsymbol{\bar y}$ by defining $\boldsymbol u = \boldsymbol{y}(\boldsymbol{w}) - \boldsymbol{\bar y}$. The flow simplifies to:
\[\boldsymbol{\dot u} = -\boldsymbol{H}(\boldsymbol{w_0}) \boldsymbol u\]The solution of this ODE is given by a matrix exponential:
\[\boldsymbol u(t) = \boldsymbol u(0)e^{-\boldsymbol{H}(\boldsymbol{w_0}) t}\]Because our model is over-parameterized ($p > n$), the NTK $\nabla \boldsymbol{y}(\boldsymbol{w_0})^T \nabla \boldsymbol{y}(\boldsymbol{w_0})$ is always positive definite (ignoring any degeneracy in the dataset that would cause $\nabla \boldsymbol{y}(\boldsymbol{w_0})$ to not have full column rank). By performing a spectral decomposition on the positive definite NTK, we can decouple the trajectory of the gradient flow into independent 1-d components (the eigenvectors) that decay at a rate proportional to the corresponding eigenvalue. The key thing is that they all decay (because all eigenvalues are positive), which means that the gradient flow always converges to the equilibrium where train loss is 0.
Through this sequence of arguments, we have shown that gradient descent converges to 0 training loss for any non-linear model as long as it is close to its linearization (which can be achieved by just taking the scale $\alpha \to \infty$)! This is the essence of most of the proofs in the recent papers which show that gradient descent achieves 0 train loss.
Seeing the Kernel Regime
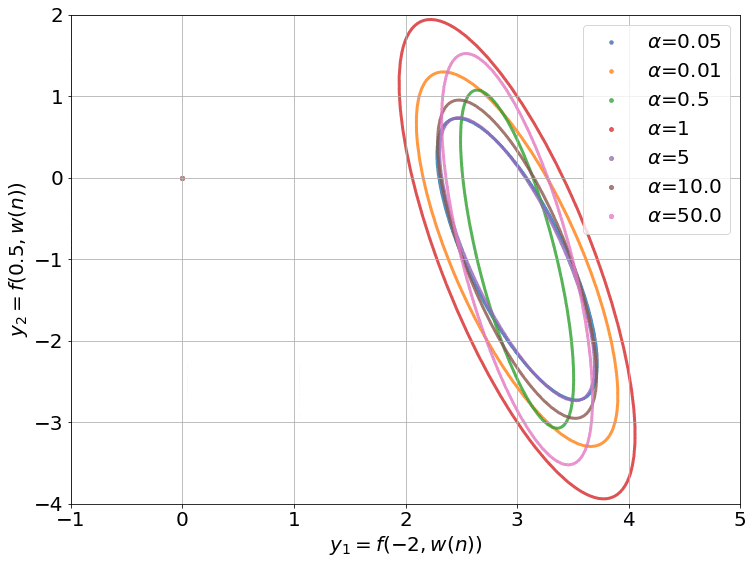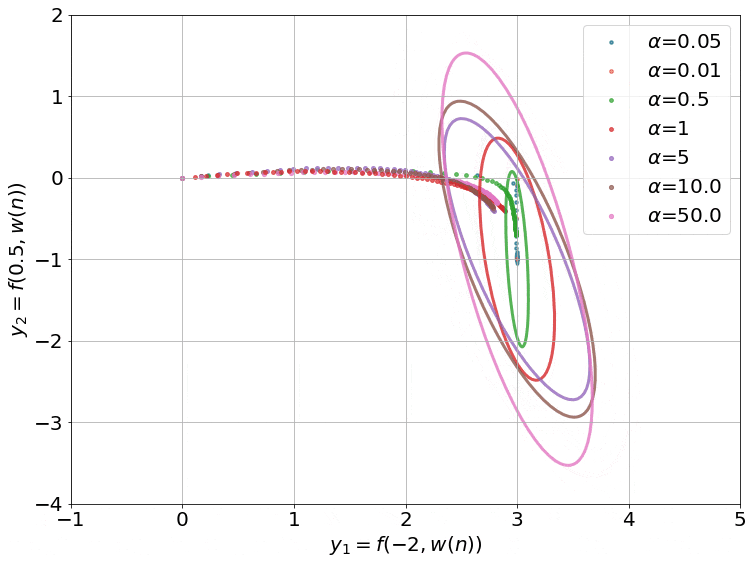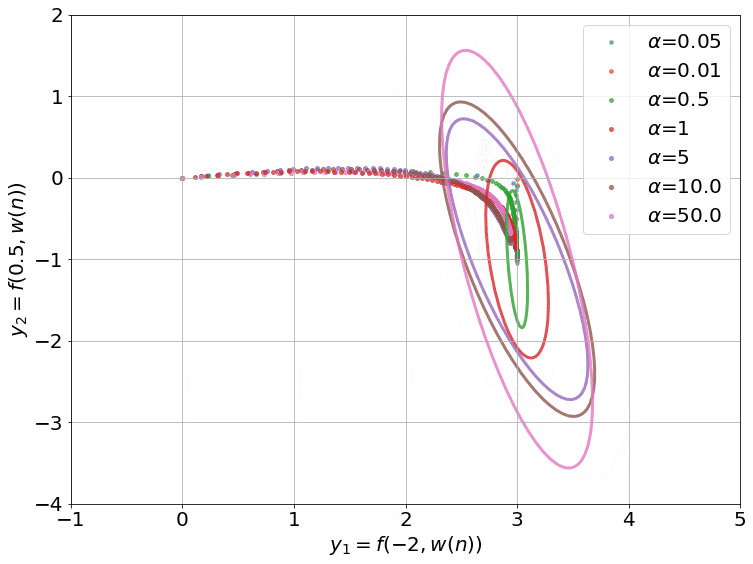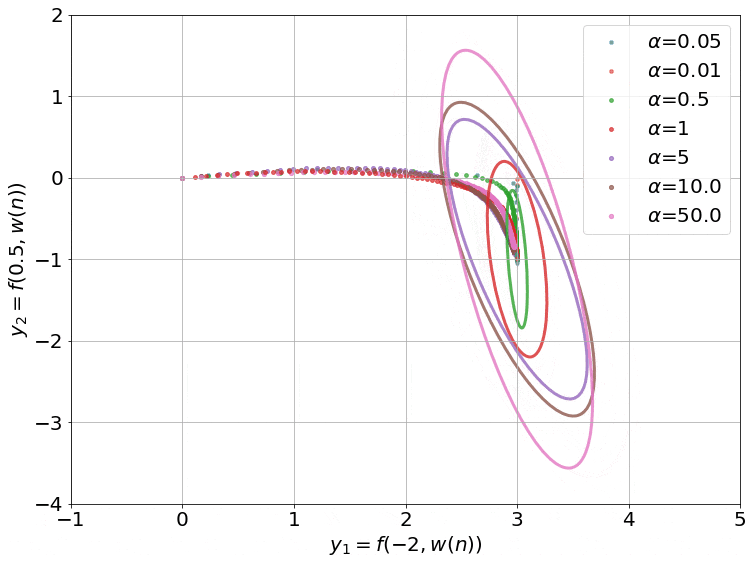
The gradient flow math can be a bit overwhelming, so let’s try to grab a handle on what’s going on by going back to our 2-dataset example. For 2 data points, the NTK is just a 2x2 positive definite matrix. We can visualize such matrices as ellipses in a 2-D plane, where the major and minor axes are the eigenvectors, and their lengths are inversely proportional to the square root of the eigenvalues. The ellipse is basically a contour of the time-varying quadratic $(\boldsymbol y - \boldsymbol{\bar y})^T \boldsymbol H( \boldsymbol w(t)) (\boldsymbol y - \boldsymbol{\bar y})$.
On top of this, we can visualize the trajectory of $\boldsymbol y( \boldsymbol w(t))$ induced by gradient descent (which approximates gradient flow) on this 2-D plane as well. This trajectory is equivalent to performing gradient descent on the same time-varying or instantaneous quadratic. This is how it looks:

- I intentionally centered the ellipses on the target data $\boldsymbol{\bar y}$ so that the trajectories would approach the center. This way, you can see that the component corresponding to the shorter axis (larger eigenvalue) of the ellipse converges faster than the longer axis (smaller eigenvalue).
- The smaller values of $\alpha$ also converge to 0 train loss (this is called the ‘deep’ or ‘rich’ regime). We don’t have any theoretical justification for this, though. Our proof only works when $\alpha$ is large enough for the ellipse to stay constant throughout training (kernel regime).
- The smallest $\alpha$’s converge so fast it’s barely possible to notice in the gif.
- I used a two hidden layer network with a width of 100 for these runs. I also zeroed the outputs of these networks by subtracting a copy at initialization (that is why all the trajectories start from the origin). While we can’t visualize how the 10000 or so weights of this network move as we train, we can visualize the networks outputs, and that is what this gif does.
The main takeaway is this: the kernel regime does occur as we expected for large alpha, but the behavior for small alpha escapes a theoretical explanation.
An additional point:
The NTK regime in these plots occur for large $\alpha$. We could also approach this regime by taking the width to infinity as we showed earlier instead of just scaling the output. However, we get a special bonus in this case. Notice that the NTKs at initialization are different, this is because the initialization is random. But, as we take the hidden widths to infinity in a neural network, it turns out that the kernel at initialization becomes deterministic! There is one fixed NTK for a given depth and activation function. In fact, this NTK can actually be computed exactly, effectively simulating an infinite width neural network (see this paper On Exact Computation in an Infinitely Wide Net). This result is very similar to the deterministic gradient norm we saw in the one hidden layer network proof above, but I won’t go into further details, because this post is long enough already.
Generalization
So far, we only talked about what happens for the training data. But what about the test set, i.e. the points in between our training samples?
Firstly, training the model in the kernel regime is equivalent to solving a linear system. Over-parameterization ($p>n$) just means that this linear system is under-determined – so it has infinite solutions. Since we are using gradient descent to solve this system, it is implicitly biased towards a solution of minimum norm. That is, gradient descent chooses that solution which has minimum $\Vert \boldsymbol w \Vert_2$ (as long as we start from an initialization with low norm).
If we now think of extending the $\boldsymbol y$-space to a function space of infinite dimension, then this minimum $\ell_2$ norm in $w$-space translates to choosing a function that minimizes a specific functional norm. What determines this norm? The kernel which describes the linear problem does, which in this case is the NTK. This can then be interpreted as a form of regularization, and you can use this to talk about generalization. I won’t delve into further details, as this post is mainly aimed at understanding optimization results as opposed to generalization. If you want to learn more about this, I’d suggest looking up stuff on reproducing kernel Hilbert spaces and the generalizing properties of kernel machines.
Concluding Remarks
The NTK theory is great, but the above visualizations show that there is more to neural networks than just this kernel regime. Experiments show that practically successful neural networks definitely do not operate in the kernel regime. In fact, even the best linearized neural networks (exactly computed NTKs for infinite width) actually perform worse on standard benchmarks like MNIST and CIFAR by around ~7% (although recent developments might have bridged this gap, see this paper on Enhanced Convolutional NTKs).
However, this NTK regime theory is not the only theory for understanding neural network training dynamics. There is also a line of work (see references) that uses ideas from optimal transport and mean field theory to characterize the dynamics when the model scaling is not large ($\kappa \sim 1$) through a non-linear PDE, but to my knowledge, these theories don’t extend beyond networks with a single hidden layer.
Nevertheless, these NTK results are still extremely interesting, because they offer a new perspective on neural network learning. Trying to understand how the kernel changes as training progresses seems like an important question to answer in the search for a better theory of neural networks.
You can find the code for this post in this repo.
Special thanks to my brother Anjan and my guide Prof. Harish Guruprasad for their insightful comments and suggestions.
References
Related to NTK:
- This nice YouTube video by Arthur Jacot summarizes the NTK paper and also has some more visualizations which I didn’t present in this post.
- Jacot, Arthur, Franck Gabriel, and Clément Hongler. “Neural tangent kernel: Convergence and generalization in neural networks.” Advances in neural information processing systems. 2018.
- Chizat, Lenaic, and Francis Bach. “A note on lazy training in supervised differentiable programming.” arXiv preprint arXiv:1812.07956 (2018).
- Arora, Sanjeev, et al. “On exact computation with an infinitely wide neural net.” arXiv preprint arXiv:1904.11955 (2019).
- Li, Zhiyuan, et al. “Enhanced Convolutional Neural Tangent Kernels.” arXiv preprint arXiv:1911.00809 (2019).
Mean field dynamics and optimal transport point of view:
- Chizat, Lenaic, and Francis Bach. “On the global convergence of gradient descent for over-parameterized models using optimal transport.” Advances in neural information processing systems. 2018.
- Mei, Song, Theodor Misiakiewicz, and Andrea Montanari. “Mean-field theory of two-layers neural networks: dimension-free bounds and kernel limit.” arXiv preprint arXiv:1902.06015 (2019).